Mi Diario de Clase

 Funciones Lineales y Polinomiales

Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma

siendo $m\ne 0$.

• $m$ es la pendiente de la función
• $n$ es la ordenada (en el origen) de la función

La gráfica de una función lineal es siempre una recta.

Ejemplo

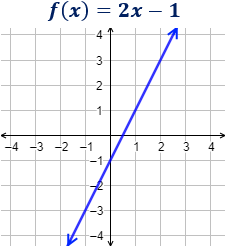
La pendiente de la función es $m=2$ y la ordenada es $n=-1$.

La pendiente es el coeficiente de la variable, es decir, $m$.

Geométricamente, cuanto mayor es la pendiente, más inclinada es la recta. Es decir, más rápido crece la función.

• Si la pendiente es positiva, la función es creciente.
• Si la pendiente es negativa, la función es decreciente.

Ejemplo

Rectas con pendientes 1, 2, 3 y -1:

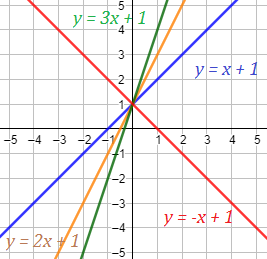
Observad que la recta con pendiente negativa $-1$ es decreciente (la roja). Las otras tres rectas son crecientes.

De las rectas crecientes, la que crece más rápidamente es la verde (pendiente $3$).

Gráfica

Como una función lineal es una recta, para representar su gráfica sólo tenemos que trazar la recta que une dos de sus puntos. Para ello, calculamos la imagen de dos puntos cualesquiera.

Ejemplo

Vamos a representar la gráfica de la función

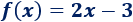
Hacemos una tabla para calcular dos puntos de la gráfica:

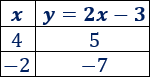
Representamos la recta a partir de los puntos $(4,5)$ y $(-2,-7)$:

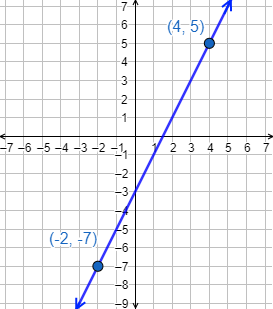
Observa que la recta corta al eje Y por debajo del eje X, esto se debe a que la ordenada es negativa ($n=-3$).

BIBLIOGRAFIA

• Casteleiro Villalba, José Manuel (2008). La matemática es fácil. Esic. ISBN 978-84-7356-533-2.
• Del Pozo García, Eva María (2004). Matemáticas fundamentales para estudios universitarios. Pearson Educación. ISBN 84-933631-6-2.