calculo de volumen por secciones transversales

 el dia 29 de octubre inciamos viendo el tema de calculo de volumen por secciones transversales con el metodo de rebanadas.

pero antes de que inicie con lo mas importante del tema, investigue las diferentes formulas para obtener el volumen de distintas figuras.

esto es sumamente importante para saber como calcular el volumen atraves de distintos metodos.

1. Determine el volumen de un sólido integrando una sección transversal (el método de rebanado).
2. Encontrar el volumen de un sólido de revolución usando el método del disco.
3. Encontrar el volumen de un sólido de revolución con una cavidad utilizando el método de arandelas.

En la sección anterior, usamos integrales definidas para encontrar el área entre dos curvas. En esta sección, usamos integrales definidas para encontrar volúmenes de sólidos tridimensionales. Consideramos tres enfoques (corte, discos y arandelas) para encontrar estos volúmenes, dependiendo de las características del sólido.

Volumen y el método de corte (rebanadas)

Así como el área es la medida numérica de una región bidimensional, el volumen es la medida numérica de un sólido tridimensional. La mayoría de nosotros hemos calculado volúmenes de sólidos usando fórmulas geométricas básicas. El volumen de un sólido rectangular, por ejemplo, se puede calcular multiplicando la longitud, el ancho y la altura: V = lwh.

Las fórmulas para el volumen de una esfera

un cono

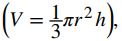
y una pirámide

También se han introducido. Aunque algunas de estas fórmulas se obtuvieron usando solo geometría, todas estas fórmulas se pueden obtener mediante la integración.

ejemplo

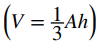
Sabemos por la geometría que la fórmula para el volumen de una pirámide es V = (1/3)Ah. Si la pirámide tiene una base cuadrada, esto se convierte en V = (1/3)a2h, donde a denota la longitud de un lado de la base. Usaremos el método de corte para derivar esta fórmula.

Solución:

Queremos aplicar el método de corte a una pirámide con una base cuadrada. Para configurar la integral, considere la pirámide que se muestra en la Figura 6.6, orientada a lo largo del eje x.

(Figura 6.6 (a) Una pirámide con una base cuadrada está orientada a lo largo del eje x. (b) Una vista bidimensional de la pirámide se ve de lado.)

Primero queremos determinar la forma de una sección transversal de la pirámide. Sabemos que la base es un cuadrado, por lo que las secciones transversales también son cuadrados (paso 1). Ahora queremos determinar una fórmula para el área de uno de estos cuadrados transversales. Mirando la Figura 6.6 (b), y usando una proporción, dado que estos son triángulos semejantes, tenemos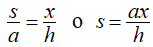

Por lo tanto, el área de uno de los cuadrados de sección transversal es

Luego encontramos el volumen de la pirámide integrando de 0 a h (paso 3):

Esta es la fórmula que estábamos buscando.

bibliografia

• Pita Ruiz, Claudio (1995): "Cálculo Vectorial". Prentice Hall.
• Sanz, Paloma; Vázquez, Francisco José (1995): "Cuestiones de Cálculo". Pirámide.
• Stewart, James (1999): "Cálculo. Transcendentes tempranas". 4ª edición. Thomson.
• Stewart, James (2001): "Cálculo de una variable. Transcendentes tempranas". 4ª edición. Thomson.
• Stewart, James (2001): "Cálculo multivariable". 4ª edición. Thomson.